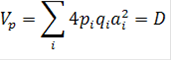Общую комбинационную способность (ОКС), как правило, устанавливают на основе топкроссных испытаний. Для определения специфической комбинационной способности (СКС) необходимы диаллельные скрещивания, которые включают в себя все возможные комбинации скрещивания между серией сортов и линий. Соответствующие методы определения комбинационной способности разработал Б. Гриффинг, предложивший четыре метода анализа диаллельного скрещивания:
Заказать имплантация зубов в уфе по цене novikovski-stomatology.ru/implant.
. Изучают родительские формы, F1 - гибриды прямых и обратных скрещиваний всего m2 генотипов.
2. Изучают родительские формы и F1 полученные в результате прямых скрещиваний, - всего m(m+1)/2 генотипов.
3. Изучают только прямые и обратные гибриды F1 - всего m(m-1) генотипов.
4. Изучают только прямые гибриды F1 - всего m(m-1)/2 генотипов.
Для анализа комбинационной способности в целях гетерозисной селекции, как правило, применяют метод IV.
Топкроссы применяют для определения общей и специфической комбинационной способности при селекции на гетерозис. Для этого линии и сорта скрещивают с одним или несколькими сортами - анализаторами (тестерами). При этом в селекции самоопыляющихся растений большое значение имеет определение эффектов общей комбинационной способности, по величине которых можно судить о донорских свойствах скрещиваемых форм [1].
Поликросс требует определенной подготовительной работы и планирования. Однако при использовании поликросса не требуется проводить оценку комбинационной способности родителей. Применяется главным образом к тем перекрестноскрещивающимся культурам, у которых получение семян от контралируемых скрещиваний затруднено. Результаты поликроссного испытания указывают на сорта, имеющие повышенную комбинационную способность, которые затем рекомендуют в состав синтетической популяции. По методам Гриффинга возможны два варианта оценки исходного материала. Вариант I (модель I) применяют, когда родительские формы для исследования отбирают специально и необходимо оценить их комбинационную способность. Формы одновременно являются тестерами, с помощью которых выявляют комбинации скрещиваний. Вариант II (модель II) используют, когда родительские формы отобраны случайно из популяции, которые необходимо оценить (тестером служит исследуемая родительская популяция). Исходные линии случайно отобраны из популяции, полученной длительным самоопылением (без отбора) генотипов исследуемой популяции. В данном случае представляют интерес не сами пара - метры отдельных родительских линий, а компоненты генотипической и дисперсии признака в исходной популяции. Значение признака для гибридной комбинации между i-м j -м родительским сортом в k-м повторении можно выразить в биометрической модели следующий вид уравнения (6):
xijk=µ+gi+gj+sij+ri+ek (6)
где хijk- величина признака у гибрида F1 между i-й и j-й родительскими линиями в k-м повторении; µ- среднее значение признака в наборе линий и гибридов F1, gi , gj эффект общей комбинационной способности i-й и j-и родительских линии; sij - эффект специфической комбинационной способноcти; ri - реципрокный эффект при скрещивании i-й и j-й линий; ек- эффект, обусловленный случайной ошибкой в k-м повторении.
Существенность отношения определяемая по Р - критерию Фишера, указывает, что между исследуемыми гибридами (или гибридами и линиями) имеются различия по величине признака, случайные ошибки опыта. Если различия не значимы, дальнейший анализ комбинационной способности не проводят. Оценки и их разности, необходимые для дальнейшего анализа, несут случайные ошибки, которые характеризуются дисперсиями ошибок (var) (7):
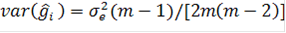 (7)
(7)
Третий метод Гриффинга. Оценка одного из вкладов в дисперсию СКС меньше нуля. Это объясняется неучтенными ошибками опытов и, возможно, неполным соответствием данных стандартным предположениям дисперсионного анализа [1].
Теоретическая основа метода Хеймана. Данный метод базируется на предположении, что количественный признак детерминирован k полиморфными локусами, точнее блоками сцепленных полигенов. Каждый локус в анализируемом наборе из родительских линий может иметь два аллельных состояния. Вклад этих генных различий в оценки статистических параметров, сред - них, дисперсий, ковариаций будут следующими (без учёта ошибок опытов). Дисперсия величин признака у родительских линий (8):
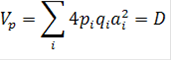
где ∑ - сумма по всем k полиморфным локусам; D - изменчивость аддитивных эффектов аi у родителей с учетом частот pi и qi
Метод Хеймана можно рассмотреть и как генетический анализ популяции. Из уравнении следует, что при выполнении требований на Э влияют только аддитивные, а на Н1 и Н2 - доминантные эффекты. Отношение характеризует степень доминирования в экспериментальном материале, среднюю по всем полиморфным локусам.
Отношения позволяют сделать выводы относительно генетической детерминации количественного признака у изученных родительских форм. В этом состоит так называемый параметрический вариант метода Хеймана. Используется также регрессионный анализ Хеймана. Метод Хеймана обладает определенной робастностью - устойчивостью к неполному удовлетворению шести требований. Вопрос о проверке выполнения требований и о пределах устойчивости выводов до настоящего времени решен не полностью. Сравнительно низкие требования к объёму и структуре эксперимента позволяют методу Хеймана оставаться популярным в селекционно-генетических исследованиях растений [1].
 TimeBiology
TimeBiology